58  Anscombe’s quartet

Author

Andres Patrignani

Published

January 15, 2024

Keywords

plotting, correlation, graphs, regression

In 1973, English statistician Francis John Anscombe emphasized the crucial role of graphical analysis in statistics through a seminal paper where he argued that visual inpsection of data through graphs not only reveals unique insights but also the main characteristics of a dataset. To illustrate his point, Anscombe created a synthetic dataset, known as Anscombe’s quartet, consisting of four distinct pairs of x-y variables. Each of the four datasets in the quartet has the same mean, variance, correlation, and regression line:

Question: Despite their identical statistical metrics, can these four datasets considered similar?

# Import modules
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
# Load Ascombe's dataset
df = pd.read_csv('../datasets/anscombe_quartet.csv')

# Display entire dataset
df.head(11)
obs x1 y1 x2 y2 x3 y3 x4 y4
0 1 10 8.04 10 9.14 10 7.46 8 6.58
1 2 8 6.95 8 8.14 8 6.77 8 5.76
2 3 13 7.58 13 8.74 13 12.74 8 7.71
3 4 9 8.81 9 8.77 9 7.11 8 8.84
4 5 11 8.33 11 9.26 11 7.81 8 8.47
5 6 14 9.96 14 8.10 14 8.84 8 7.04
6 7 6 7.24 6 6.13 6 6.08 8 5.25
7 8 4 4.26 4 3.10 4 5.39 19 12.50
8 9 12 10.84 12 9.13 12 8.15 8 5.56
9 10 7 4.82 7 7.26 7 6.42 8 7.91
10 11 5 5.68 5 4.74 5 5.73 8 6.89 
# Define a linear model
lm = lambda x,intercept,slope: intercept + slope*x
# Fit linear model to each dataset
slope_1, intercept_1, r_val_1, p_val_1, std_err_1 = stats.linregress(df.x1, df.y1)
slope_2, intercept_2, r_val_2, p_val_2, std_err_2 = stats.linregress(df.x2, df.y2)
slope_3, intercept_3, r_val_3, p_val_3, std_err_3 = stats.linregress(df.x3, df.y3)
slope_4, intercept_4, r_val_4, p_val_4, std_err_4 = stats.linregress(df.x4, df.y4)
# Plot points and fitted line
plt.figure(figsize=(8,8))

plt.subplot(2,2,1)
plt.title('Group 1')
plt.scatter(df['x1'], df['y1'], facecolor='w', edgecolor='k')
plt.plot(df['x1'], lm(df['x1'],intercept_1, slope_1), color='tomato')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([0,20])
plt.ylim([0,15])
plt.text(2,14, f"Mean={df['y1'].mean():.1f}")
plt.text(2,13, f"Variance={df['y1'].var():.1f}")
plt.text(2,12, f"r={r_val_1:.2f}")
plt.text(2,11, f"y={intercept_1:.1f} + {slope_1:.1f}x")

plt.subplot(2,2,2)
plt.title('Group 2')
plt.scatter(df['x2'], df['y2'], facecolor='w', edgecolor='k')
plt.plot(df['x2'], lm(df['x2'],intercept_2, slope_2), color='tomato')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([0,20])
plt.ylim([0,15])
plt.text(2,14, f"Mean={df['y2'].mean():.1f}")
plt.text(2,13, f"Variance={df['y2'].var():.1f}")
plt.text(2,12, f"r={r_val_2:.2f}")
plt.text(2,11, f"y={intercept_2:.1f} + {slope_2:.1f}x")

plt.subplot(2,2,3)
plt.title('Group 3')
plt.scatter(df['x3'], df['y3'], facecolor='w', edgecolor='k')
plt.plot(df['x3'], lm(df['x3'],intercept_3, slope_3), color='tomato')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([0,20])
plt.ylim([0,15])
plt.text(2,14, f"Mean={df['y3'].mean():.1f}")
plt.text(2,13, f"Variance={df['y3'].var():.1f}")
plt.text(2,12, f"r={r_val_3:.2f}")
plt.text(2,11, f"y={intercept_3:.1f} + {slope_3:.1f}x")

plt.subplot(2,2,4)
plt.title('Group 4')
plt.scatter(df['x4'], df['y4'], facecolor='w', edgecolor='k')
plt.plot(df['x4'], lm(df['x4'],intercept_4, slope_4), color='tomato')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim([0,20])
plt.ylim([0,15])
plt.text(2,14, f"Mean={df['y4'].mean():.1f}")
plt.text(2,13, f"Variance={df['y4'].var():.1f}")
plt.text(2,12, f"r={r_val_4:.2f}")
plt.text(2,11, f"y={intercept_4:.1f} + {slope_4:.1f}x")

plt.subplots_adjust(wspace=0.3, hspace=0.4) 
plt.show()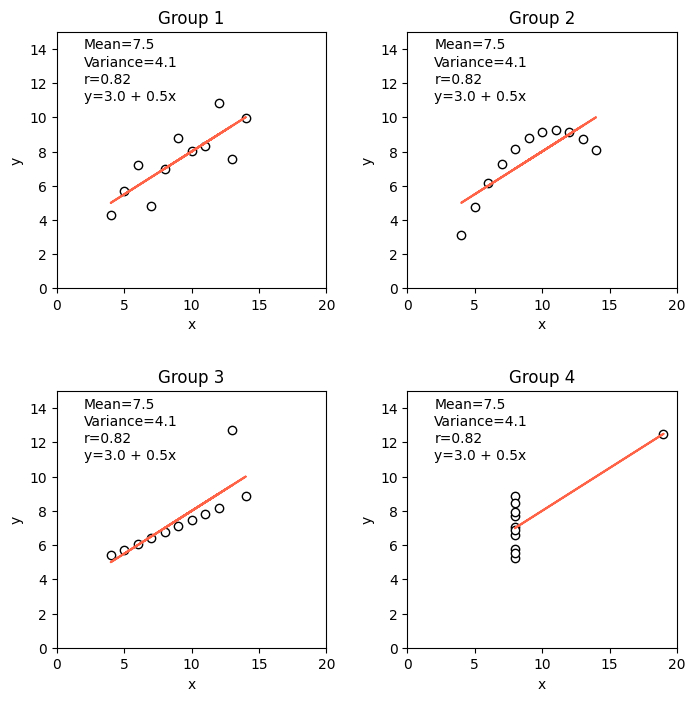

Practice

  • Compute the root mean square error, mean absolute error, and mean bias error for each dataset. Can any of these error metrics provide a better description of the goodness of fit for each dataset?

  • Instead of creating the figure subplots one by one, can you write a for loop that will iterate over each dataset, fit a linear model, and then populate its correpsonding subplot?

References

Anscombe, F.J., 1973. Graphs in statistical analysis. The American Statistician, 27(1), pp.17-21.